This practice consists of local robot navigation technique using VFF. The aim is that the robot reaches a certain site that we have stated autonomously, avoiding obstacles that meet on the road. This technique involves virtual attractive and repulsive forces. In this case, the attractive force is generated by the destination you want to go, and is generated by repulsive obstacles so that adding the two forces we get a vector that tells us where to go at all times.
That is, the robot will go according to the force resulting from adding the attractive and repulsive force total. 
This resultant force depends on the importance we place on the attractive force against the repulsive, because if we attach great importance to the attractive force can make the robot is too reckless and ends colliding with obstacles. In contrast, if we give too much importance to the repulsive force, we run the risk of being too cautious and does not reach certain destinations, or does not pass through places that could easily pass. How forces are generated?
The attractive is generated from the point where we go. Creates a vector on the robot in which direction is the line connecting the destination with the robot, and the length or intensity is the distance that is.
In my case I have decided that the maximum force is 700, ie if the destination is more than 700mm the attractive force is 700, and if it is less distance is equal to the distance that is.
This means that when the robot is near the target the attractive force is smaller and thus the robot is more carefully and more slowly (below I explain the rates at which it moves).
The repulsive force is generated from nearby obstacles, which are detected by laser.
Each of the 180 laser robot tells us the distance that is an obstacle if any, so they generate the repulsive force is more difficult to generate the attractive force for three reasons:
- There are 180 measures they have to look
- The force generated by adding lasers indicates where we should not go, so you need to do to "flee" from that direction, we must reverse the vector.
- information that gives us the laser is the distance that is the obstacle, but the farther away you are, the less we repel, so that the force generated by each laser is inversely proportional to the distance that you provide.
In my case I have only considered the obstacles that are less than 1000 mm, and the repulsive force that grows quadratically generated, so that the closer the obstacle strength is even higher.
To obtain the total repulsive force add all the vectors generated the above form and invest the vector.
to invest simply change the sign to the coordinates x and y.
The way to add vectors is a sum of trigonometric vectors.
If I have two vectors A and B where A = ax +
by
B = cx + dy
C = A + B = (a + c) x + (b + d) and
This example, summary the red and blue vector and the vector would result in green.
Because each laser measurement we obtain the coordinates of the obstacle (relative to the robot) in polar coordinates, we must make a transformation from polar coordinates to Cartesian coordinates. To do this we have (
r, θ) where r is the distance to the obstacle and the angle θ respect to the robot. obtain Cartesian coordinates as the following two equations.
-
-
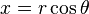
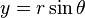Once done do the vector sum.
f = k * (1/laser [i]) ^ 2 The constant k I have chosen is 1600000.
The following pictures show how it grows much faster than the repulsive force the closer the robot to the obstacle (the repulsive force is the blue line).
When moving the robot to distinguish several cases:
"If the force is between 15 º and -15 º, the robot moves forward at a rate equal to the intensity of the resultant force
- If the force is between 15 º and 180 º the robot turns left, with a speed 20 times the angle (in radians) which is the resultant force, so that the more degrees you have to rotate, faster turns. The speed at which progress also depends on the angle you have to turn, because the more you have to turn the slower.
If you have to rotate over 103 ° the rate is 10 mm / s, if less advance at a rate inversely proportional to speed, I have used the following formula:
v = fTotal * 1.5 / w
provided that the result is greater than 35, but the speed be 35 because otherwise the robot would move very slowly without having to go so slowly
- If the force is between 180 º and 345 º the robot turn right in a manner similar to the previous.
The next problem to solve is the condition of stopping the robot, and knows he has reached the destination.
I think it reaches the destination where the resultant force is less than 60, and the attractive force less than 500.
Problems:
If access to the destination, the robot has an obstacle in the way, it is possible to set aside the total force to offset the attractive force and repulsive. You may also not defeated, but can make robot rotate to one side and turn to that side of the resultant force him to turn again to indicate to the opposite side, and after it turned on, turning him back to the other side and so on so that it is turning to back and forth without moving or moving very slowly.
As shown, the attractiveness (red) and repulsive (blue) are offset and the resulting (green) virtually disappears.
To avoid this, I created a state of "stuck."
This state is triggered if the following conditions are met: - The intensity of the resultant force is less than 110
- The intensity of the attractive force is greater than 600
- The attractive and repulsive forces have approximately the same direction (other direction). I considered that this is true they vary with respect to each other less than 2.2 º.
The state is stuck for 2 seconds when the robot turns left and proceeds (provided they do not crash) trying to escape from that point where the forces vanish.
Another problem I found was that if the target is "just around the corner" of an obstacle, it was moving very slowly, because the resultant force was very small, and also saw more diminished because he had to turn, when it really could go faster. To
This put the minimum speed when turning is 35 (provided you have to turn less than 103 degrees as indicated above.
Then I put a video of the operation.